Fourier Series - Definition, Formula, Applications | Understanding the Power of Harmonic Analysis

 

Fourier Series: Understanding the Power of Harmonic Analysis

In the vast world of mathematics and signal processing, the Fourier series stands as a remarkable tool for understanding the behavior of periodic functions. With its profound implications in various fields, from physics to engineering, the Fourier series has revolutionized the way we comprehend and manipulate data. In this comprehensive article, we delve into the depths of the Fourier series, exploring its fundamental concepts, applications, and its significance in today's digital era.

What is the Fourier Series?

A Fourier series is an expansion of a periodic function f(x) in terms of an infinite sum of sines and cosines. Fourier Series makes use of the orthogonality relationships of the sine and cosine functions.

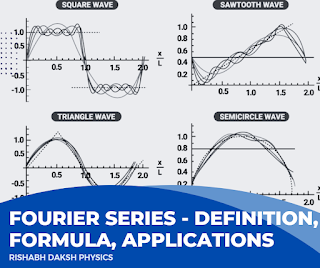Fourier Series - Definition, Formula, Applications

Also Read:

• Taylor Series
• Sine Function
• Derivative Function Calculus
• What is Electric Current ? Electric Flux, Electric Dipole Moment and Electrical Energy | Physics Class 12 CBSE Board Chapter 3 | Current Electricity Notes and PDF for free
• CBSE Class 12 Physics notes All Chapters
• Unit and Dimensions of Class 11 Physics

The General Form of the Fourier Series Equation

The Fourier series equation represents a periodic function f(x) as a sum of sine and cosine functions with different frequencies and amplitudes. The general form of the equation is as follows:

f(x) = a₀/2 + Σ(aₙcos(nω₀x) + bₙsin(nω₀x))

In this equation, the terms a₀/2, aₙ, and bₙ represent the coefficients that determine the contribution of each harmonic component. The value of ω₀ represents the fundamental frequency of the periodic function, and n denotes the harmonic number.

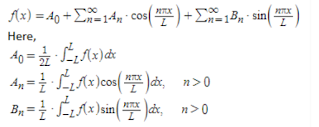Fourier series Formula

Understanding the Coefficients

a₀/2 - The DC Component: The term a₀/2 represents the average value of the function f(x) over one period. It is often referred to as the DC component since it determines the vertical shift or offset of the periodic function.

aₙ - Cosine Coefficients: The coefficient aₙ determines the amplitude of the cosine component corresponding to the harmonic number n. It captures the even symmetry in the periodic function and provides information about its overall shape and magnitude.

bₙ - Sine Coefficients: The coefficient bₙ determines the amplitude of the sine component corresponding to the harmonic number n. It captures the odd symmetry in the periodic function and provides insights into its asymmetrical characteristics.

Calculating the Coefficients

The calculation of the Fourier coefficients involves integrating the periodic function f(x) multiplied by sine and cosine functions over one period. The formulas for calculating the coefficients are as follows:

a₀ = (2/T) * ∫[T/2,-T/2] f(x) dx

aₙ = (2/T) * ∫[T/2,-T/2] f(x) * cos(nω₀x) dx

bₙ = (2/T) * ∫[T/2,-T/2] f(x) * sin(nω₀x) dx

Here, T represents the period of the function, and ω₀ = (2π)/T denotes the fundamental angular frequency.

The Significance of Different Coefficients

The coefficients in the Fourier series equation provide valuable insights into the composition and behavior of the periodic function. By examining the values of the coefficients, we can infer important characteristics such as symmetry, amplitude distribution, and phase relationships among the harmonics.

The DC component (a₀/2) helps determine the average value or the vertical shift of the function. It is essential for understanding any offset or bias in the periodic signal.

The cosine coefficients (aₙ) contribute to the even symmetry of the function. They provide information about the amplitudes of the even harmonics present in the periodic signal.

The sine coefficients (bₙ) contribute to the odd symmetry of the function. They reveal the amplitudes of the odd harmonics present in the periodic signal.

Unveiling the Essence of the Fourier Series

At its core, the Fourier series is a mathematical representation of a periodic function in terms of its harmonic components. By breaking down a complex waveform into a sum of simpler sinusoidal functions, the Fourier series provides an elegant framework for analyzing and understanding the intricate patterns hidden within the data. The series owes its name to the French mathematician and physicist Jean-Baptiste Joseph Fourier, who introduced it in the early 19th century.

The Beauty of Harmonic Analysis

Harmonic analysis, the cornerstone of the Fourier series, allows us to decompose a function into its constituent frequencies. It reveals the inherent relationship between the time domain and the frequency domain, offering valuable insights into the behavior of signals. By examining the amplitudes, phases, and frequencies of the harmonics, we can gain a profound understanding of the original function and its properties.

Applications Across Diverse Disciplines

The Fourier series finds applications in a wide array of fields, each harnessing its power to uncover hidden information and enhance our understanding. Let's explore some of the prominent applications:

1. Signal Processing: In the realm of digital signal processing, the Fourier series is instrumental in transforming signals from the time domain to the frequency domain. This transformation enables efficient filtering, noise reduction, compression, and modulation techniques.

2. Telecommunications: From voice transmission to data encoding, the Fourier series plays a vital role in modern telecommunications. By analyzing the spectral components of signals, we can optimize bandwidth allocation, design efficient modulation schemes, and enhance the overall performance of communication systems.

3. Audio and Image Compression: Fourier series-based algorithms, such as the famous Discrete Fourier Transform (DFT) and its fast variant, the Fast Fourier Transform (FFT), lie at the heart of audio and image compression techniques. These algorithms exploit the redundancy and sparsity of signals in the frequency domain, enabling efficient storage and transmission of multimedia data.

4. Partial Differential Equations: The Fourier series finds extensive use in solving partial differential equations, facilitating solutions for complex physical phenomena, including heat conduction, fluid dynamics, and electromagnetic wave propagation. By employing the Fourier series as a powerful mathematical tool, engineers and scientists can unlock valuable insights into the behavior of these systems.

Enhancing Your Understanding of the Fourier Series

To deepen your knowledge of the Fourier series, we recommend exploring the following topics:

1. Fourier Transform: A generalized version of the Fourier series, the Fourier transform extends its application to non-periodic functions. It enables the analysis of transient signals and continuous spectra, broadening the scope of harmonic analysis.

2. Windowing Techniques: When dealing with finite-duration signals, windowing techniques, such as the Hamming or Hanning window, mitigate spectral leakage and improve frequency resolution in Fourier analysis.

3. Fast Fourier Transform (FFT): The FFT algorithm revolutionized digital signal processing, providing an efficient method for calculating the Fourier transform. Understanding the intricacies of the FFT can significantly accelerate computations in various applications.

4. Applications in Image Processing: The Fourier series finds extensive use in image processing, enabling operations like image enhancement, denoising, and feature extraction. Exploring Fourier-based techniques, such as the Fourier descriptor, can unlock exciting possibilities in the realm of computer vision.

In conclusion, the Fourier series stands as a remarkable mathematical tool that has shaped the foundations of signal processing, telecommunications, and various scientific disciplines. Its profound implications and applications continue to revolutionize the way we understand and manipulate data in our digital era. By harnessing the power of harmonic analysis, we can unlock hidden patterns, enhance our understanding of complex phenomena, and pave the way for exciting advancements across multiple fields.

Frequently Asked Questions – FAQs

Q1. What is the Fourier Series formula?

The formula for the fourier series of the function f(x) in the interval [-L, L], i.e. -L ≤ x ≤ L is given by:

f(x) = A_0 + ∑_{n = 1}^{∞} A_n cos(nπx/L) + ∑_{n = 1}^{∞} B_n sin(nπx/L)

Q2. What is the Fourier series used for?

Fourier series is used to describe a periodic signal in terms of cosine and sine waves. In other other words, it allows us to model any arbitrary periodic signal with a combination of sines and cosines.

Q3. How do you solve a Fourier series?

The steps to be followed for solving a Fourier series are given below:

Step 1: Multiply the given function by sine or cosine, then integrate

Step 2: Estimate for n=0, n=1, etc., to get the value of coefficients.

Step 3: Finally, substituting all the coefficients in Fourier formula.

Q4. What are the 2 types of Fourier series?

The two types of Fourier series are trigonometric series and exponential series.

Q5. What is meant by the Fourier series?

A Fourier series is an expansion of a periodic function f(x) in terms of an infinite sum of sines and cosines. Fourier Series makes use of the orthogonality relationships of the sine and cosine functions.